Skip to main content
high contrast version
menu

Web Content Display Web Content Display

Jagiellonian

Quantum Information Team

Breadcrumb Breadcrumb

Web Content Display Web Content Display

Web Content Display Web Content Display

Jagiellonian Quantum Information Team

We study theoretical issues related to exploiting quantum effects to encode, transmit, store, hide or delete quantum information. Thus, we analyze properties of selected quantum states and quantum dynamics, useful in various tasks of quantum information processing.

Geometry of quantum states and quantum entanglement

A quantum state is a mathematical tool – a Hermitian, positive semi-definite density matrix $\rho$ – used to compute probability of a given outcome of any measurement. It is compelling to investigate geometry of the set of quantum states of order $N$. Composite quantum states are described in a Hilbert space with a tensor product structure, e.g. $\mathcal{H}_A \otimes \mathcal{H}_B$. A state with classical correlations can be represented as a convex combination of product states, $\rho^{AB}_{\texttt{sep}}= \sum_{j=1}^k q_j \; \rho_j^A \otimes \rho_j^B$, and is called separable. All other states display quantum correlations and are called entangled [1]. Key questions one may ask concern the volume and the structure of the set of entangled states.

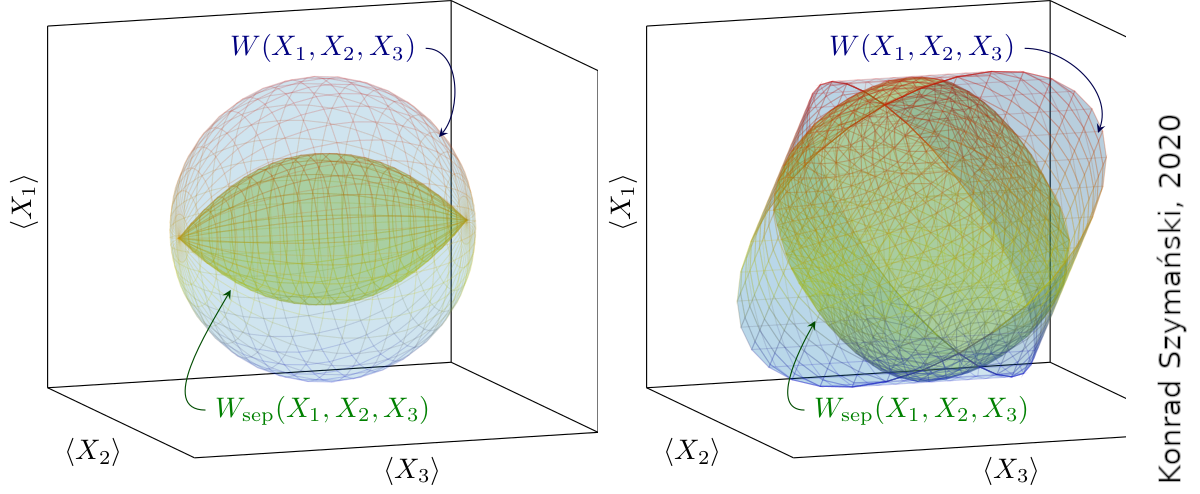
The convex set $\Omega_N$ of quantum states of order $N$ has $N^2-1$ dimensions. In the case of a single qubit it forms the Bloch ball, $\Omega_2=B_3$, with the pure states comprising the Bloch sphere. To investigate properties of such multidimensional sets arising for $N\ge 3$ we use their projection onto a $3$-space and apply the notion of joint numerical range, $W(X_1,X_2,X_3)$, which represents the set of expectation values of three Hermitian observables, $x_i=\texttt{Tr}\rho X_i$, taken over entire set $\Omega_N$.

Numerical Range of two selected triples of 4-dim. operators.
Figure 1. The numerical range $W(X_1,X_2,X_3)$ of two selected triples of operators of order four listed here that gives a projection of the set $\Omega_4$ of $2$ qubit states onto $\mathbb{R}^3$, is shown in blue. Subsets in green represent the separable numerical range $\color{green}W_{\color{green}{sep}}$, which forms a $3D$ projection of the set $\Omega^{\texttt{sep}}_N$ of separable states. The remaining blue states are entangled. Such an approach allows one to study the dynamics of quantum entanglement.
3D model of joint numerical range of order four.
Figure 2. a) $3D$ model of the difference of two sets ${\color{blue}W} \setminus {\color{green}W_{\color{green}{sep}}}$ shown in Fig. 1.a – registering three expectation values $(x_1,x_2,x_3)$, which represent a point in this set, confirms entanglement of $\rho$. b) Model of separable join numerical range of three operators of order four generated by a 3D printer at Complexity Garage.

Distinguished, extremal quantum states and quantum operations

Consider a quantum system in an $N$-dimensional Hilbert space. If no specific constraints are imposed on the system, the Hilbert space is isotropic, hence all quantum states are equal. The situation changes, if one can identify physical subsystems. In a bipartite scenario one can distinguish, for instance, product states and maximally entangled, generalized Bell states. For a particular multipartite system, it is legitimate to ask, which state is the most entangled with respect to a given measure of entanglement. A state is called absolutely maximally entangled (AME), if it is maximally entangled with respect to any bipartite partition of the system. Such states, useful for quantum teleportation and quantum error correction, are known for the four-qutrit system, $\mathcal{H}=\mathcal{H}_3^{\otimes 4}$, and several larger systems. They do not exist for seven qubits [5], and a focus of our current research is whether such states do exist for four parties with six levels each.

A set of $3$ mutually unbiased bases (MUBs) leads an informationally complete measurement of a single qubit. Any two such orthogonal bases of are related by a unitary complex Hadamard matrix, so the uncertainty related to this joint measurement is minimal. It is simple to show that in dimension $N$ there are no more than $N+1$ MUBs. For $N=3$, $4$ and $5$ this bound is also saturated, as there exist $4$, $5$ and $6$ MUBs, respectively. For $N=6$ only $3$ MUBs are found up till now, and we would like to know how many MUBs exist in dimension six to optimize the quantum measurement scheme.

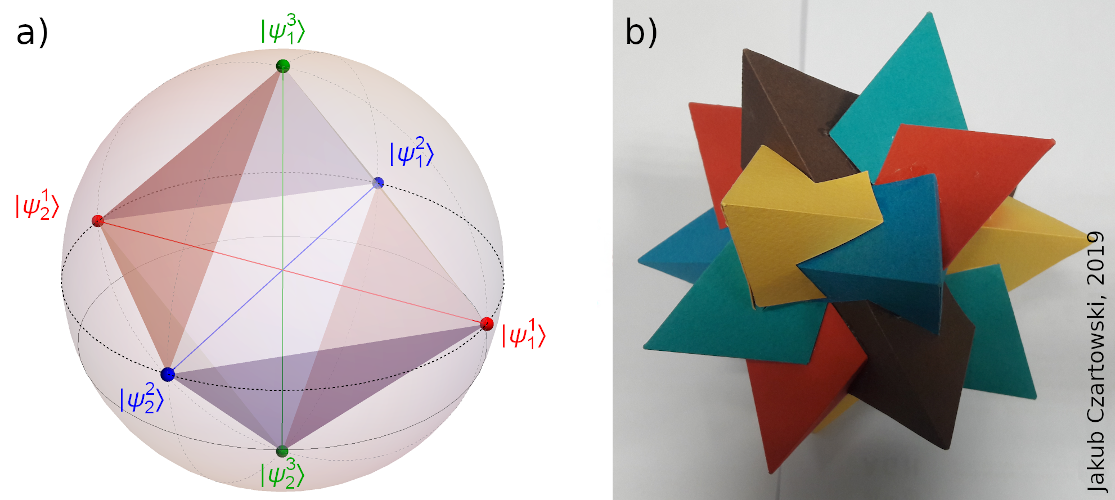
The standard construction of $5$ MUBs for a two-qubit system consists of three orthogonal bases consisting of separable states and two bases with all states maximally entangled. In [2] we found a constellation of $20$ iso-entangled states giving the full set of MUBs. Partial traces (into any subsystem) of four orthogonal states of any basis forms a regular tetrahedron inside the Bloch ball, while the corners of five such tetrahedrons yield a regular dodecahedron.

Eigenbases of three Pauli operators and a complete set of 5 isoentangled MUBs.
Figure 3. a) Eigenbases of three Pauli operators $\sigma_x$, $\sigma_y$ and $\sigma_z$ provide the complete set of $3$ MUBs for a single qubit; b) partial traces of $20$ two-qubit pure states, which form a complete set of $5$ iso-entangled MUBs in $N=4$, yield a regular dodecahedron. Any state of this unique constellation is obtained by local unitary transformations of the fiducial state \[|\phi\rangle = \frac{1}{20}\Big(a_+|00\rangle - 10i |01\rangle + (8i-6)|10\rangle + a_- |11\rangle\Big),\] where $a_\pm = -7 \pm 3\sqrt{5} + i\left(1 \pm\sqrt{5}\right)$.

To identify distinguished multipartite states, we can analyze properties of reduced density matrices. An entangled quantum state of $N$ subsystems is called $m$-resistant, if it remains entangled after losing an arbitrary subset of $m$ particles, but becomes separable after losing any number of particles larger than $m$. One can establish an analogy to the problem of designing a topological link consisting of $N$ rings such that after cutting any $(m + 1)$ of them, the remaining rings become disconnected.

book article
Borromean rings.
Figure 4. a) Borromean link forms an example of a $0$-resistant link of three rings corresponding to the polynomial ${\color{red}a}{\color{green}b}{\color{blue}c}$ and the GHZ state $$|\psi_0\rangle=|GHZ_3\rangle=\frac{1}{\sqrt{2}}\Big(|000\rangle+|111\rangle\Big).$$ b) An example of a $1$-resistant link of four rings, represented by the polynomial ${\color{red}a}{\color{green}b}{\color{blue}c}+ {\color{red}a}{\color{green}b}{\color{orange}d}+ {\color{red}a}{\color{blue}c}{\color{orange}d}+ {\color{green}b}{\color{blue}c}{\color{orange}d}$, corresponds to the $1$-resistant state of four qubits, $$|\psi_1\rangle=\frac{1}{\sqrt{20}}\Big(4|0000\rangle+|0111\rangle+|1011\rangle+|1101\rangle+|1110\rangle\Big).$$ After cutting any single ring one arrives at the Borromean link of three rings shown in panel a), while after tracing out any of four qubits, one becomes an entangled mixed state of three qubits, the entanglement of which is $0$-resistant.

Typical (random) quantum states and quantum operations

Several quantum states and operations are distinguished by attaining extremal values of quantities relevant for information processing. To provide a universal reference point we are interested in their mean values averaged over of the entire set of (pure or mixed) quantum states, computed with respect to physically motivated probability measures. These tasks can be achieved with help of the theory of random matrices. Such generic quantum states and typical quantum operations describe physical systems corresponding to classically chaotic dynamics.

Spectral properties of a quantum operation, including its spectral gap, defined as the difference between moduli of two largest eigenvalues of the superoperator, describes the convergence to the equilibrium. In the case of a discrete random operation acting on a set of states of size $N$ the spectrum consists of the leading eigenvalue, $\lambda_1=1$, and the bulk of eigenvalues in the disk of radius $R=1/N$ in the complex plane. The spectrum of a generic Lindblad operator, which describes a continuous dynamics of an open quantum system, displays a universal, lemon-like shape, discovered in [3].

Spectral density of the bulk of rescaled eigenvalues of random Lindblad operators.
Figure 5. Spectral density of the bulk of rescaled eigenvalues of random Lindblad operators generating continuous dynamics for $N = 50$ and $N=100$. Solid lines represent analytic boundaries of the lemon-like support of the spectrum derived in [3].

Quantum Resources

The first step to devise new quantum technologies able to overcome limitations of currently used classical computing machines is to identify, which components of quantum theory can provide such an advantage - we need to recognise what actually constitutes quantum resources. Once they are identified, the next step is to characterise them. Informally this corresponds to translating qualitative statements like entanglement is a useful cryptographic resource to quantitative ones like entangled state $A$ is five times better than $B$, because it allows one to securely communicate five times more bits.

More formally, characterisation requires one to understand when different resources can be interconverted and how efficiently this can be done, which is captured by the mathematical framework of resource theories. Finally, there is also the third essential step: finding optimal ways to experimentally implement protocols exhibiting quantum advantage, while taking into account realistic constraints. Our goal is to develop a theoretical framework underpinning quantum technologies, with a particular focus on quantum computing and quantum thermodynamics, by investigating all three aspects of quantum resource theories.

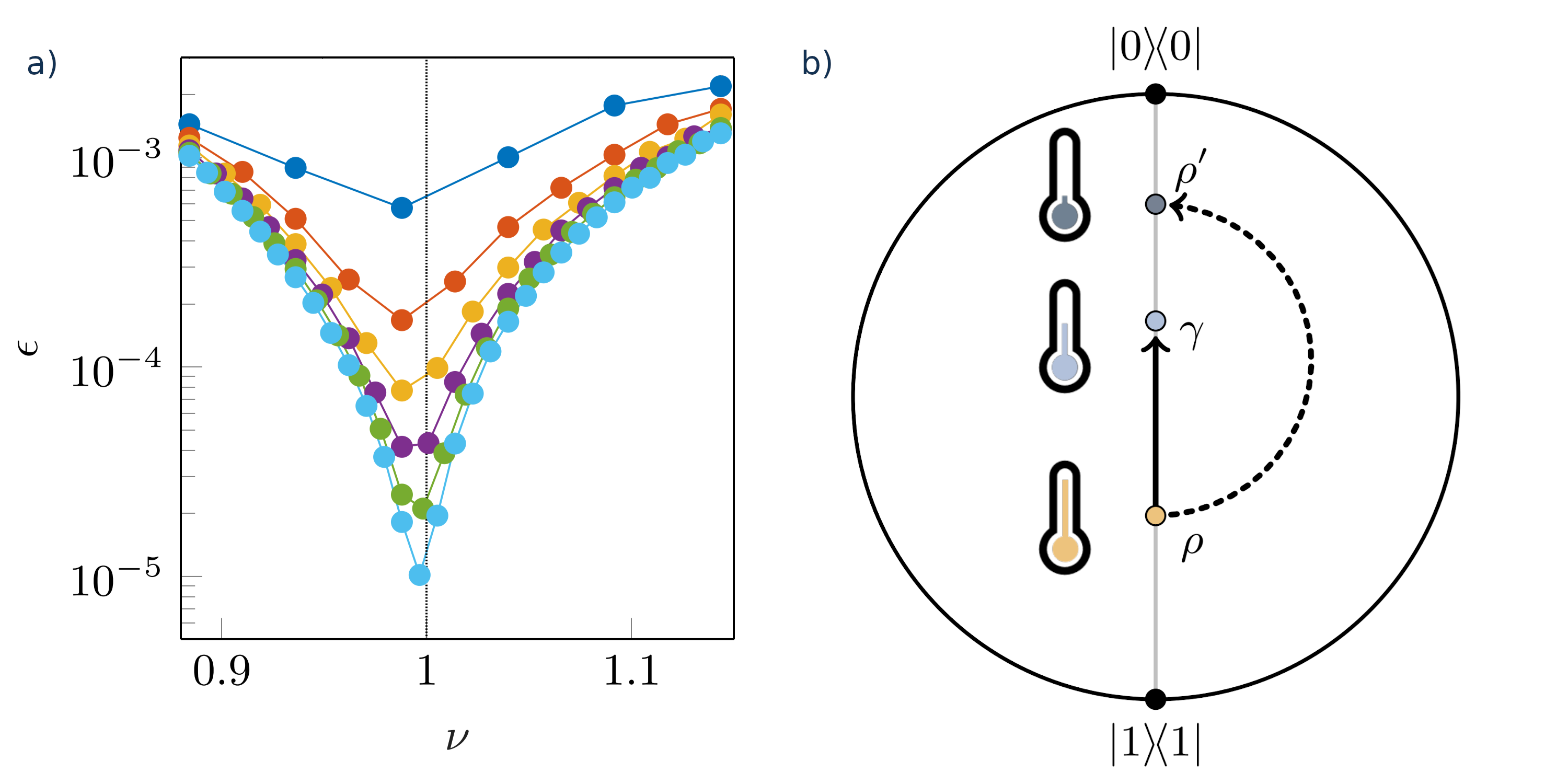
The specific research tasks include: investigating possibilities for quantum advantage within thermodynamic scenarios, developing quantitative methods to characterise resource dissipation, [4], operationally motivating coherence resources through communication scenarios, constructing experimentally feasible protocols for probing quantum thermodynamic phenomena and devising classical simulation algorithms for the certification and verification of quantum devices.

The resource resonance effect and Markovian cooling of a 2-level system. Figure 6. a) The resource resonance effect: by carefully engineering the interconversion process (controlled by irreversibility parameter $\nu$) the dissipation of resources (measured by transformation error $\varepsilon$) arising from finite-size effects can be greatly suppressed; b) Markovian cooling of a two-level system: quantum memoryless dynamics (dotted arrow) allows one to cool the system below the lowest temperature achievable by classical memoryless dynamics (solid arrow).

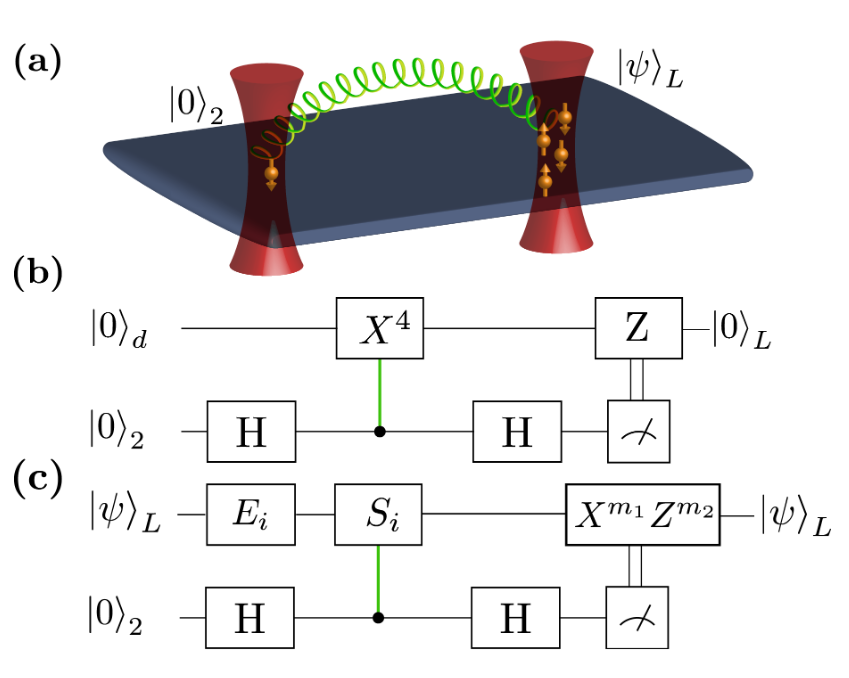
Quantum Error Correction

Similarly to a phone line that has a "bad connection" or a corrupted computer memory, quantum information can be affected by environmental noise and imperfect information processing. Quantum error correction allows the packaging quantum information in interesting ways, such that it can be safely stored and transmitted, forming a back-end to practically all types of quantum communication and computation. The existence and performance of quantum codes is related to many interesting topics in quantum information theory, such as entanglement and the sharing of quantum correlations, ground states of local Hamiltonians, and the quantum marginal problem.

Experimental implementation of quantum error correction in a ultracold atomic mixture.
Figure 7. Experimental implementation of quantum error correction in a ultracold atomic mixture: (a) The phonons of the bosonic bath couple a tweezer with $N$ atoms to a tweezer with one atom. (b) Preparation of the logical state using a control qubit and quantum gates. (c) Error correction on the encoded state.

Together with mathematicians from the Jagiellonian University and other places in Poland and abroad we also analyze various mathematical aspects of quantum information. Our joint weekly seminar has been running since 1995: Quantum Chaos and Quantum Information.

Operation entropy - illustrative scheme.
Figure 8. In search for optimal bounds for operation entropy of complementary quantum channels.

Further reading

[1] I. Bengtsson and K. Życzkowski, Geometry of Quantum States: An Introduction to Quantum Entanglement, Cambridge University Press, 2005; II ed. 2017.

[2] J. Czartowski, D. Goyeneche, M. Grassl, K. Życzkowski, Iso-entangled mutually unbiased bases, symmetric quantum measurements and mixed-state designs, Phys. Rev. Lett. 124, 090503 (2020).

[3] S. Denisov, T. Laptyeva, W. Tarnowski, D. Chruściński and K. Życzkowski, Universal spectra of random Lindblad operators, Phys. Rev. Lett. 123, 140403 (2019).

[4] K. Korzekwa, C. Chubb and M. Tomamichel, Avoiding irreversibility: engineering resonant conversions of quantum resources, Phys. Rev. Lett. 122, 110403 (2019).

[5] F. Huber, O. Gühne, and J. Siewert, Absolutely Maximally Entangled States of Seven Qubits Do Not Exist, Phys. Rev. Lett. 118, 200502 (2017).

Acknowledgments

We are grateful for the support by the following research projects:

Jagiellonian Quantum Information Team
ul. prof. S. Łojasiewicza 11
30-348 Kraków
coordinates: 50.028789, 19.905403
© 2010-2023 Jagiellonian University in Kraków, JU Website
Privacy Policy Cookie settings